[NLP][ML] Transformer (3) - More conputational detail
Overview
In this article, I will focus more on the computing detail in transformer.
It will cover self-attention, prallel processing, multi-head self-attention, positional encoding and so on.
Self-Attention
Idea
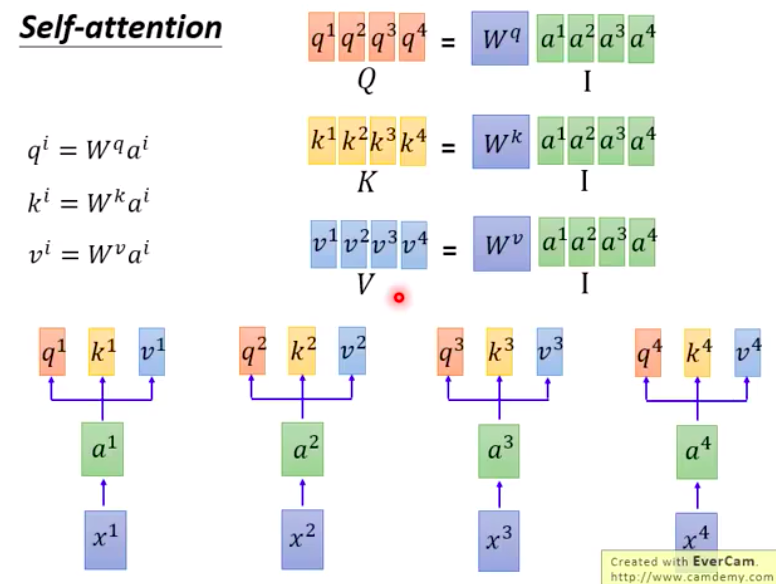
- Input:
- $x_1$, …, $x_4$, is a sequence.
- Each input first goes through an embedding(convert to vectors), multiplied by a weight matrix to become $a_1$, …, $a_4$. These $a_1$, …, $a_4$ are then passed into a Self-attention layer
- Each input is multiplied by different vectors:
- $q$: query (to match against others)
- $q_i$ = $W^qa_i$
- $k$: key (to be matched)
- $k_i$ = $W^ka_i$
- $v$: value, information to be extracted
- $v_i$ = $W^va_i$
- $q$: query (to match against others)
- The weights $W^q$, $W^k$, $W^v$ are learned, initially randomly initialized.
Method
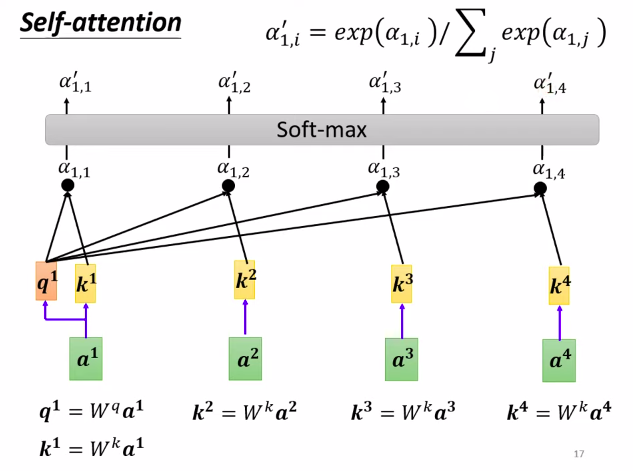
- Take each query $q$ and perform attention on each key $k$ (using two vectors to output a score(attention score)), which is essentially calculating the similarity of $q$ and $k$ (Similarity).
- Scaled Dot-Product: $S(q_1, k_1)$ yields $\alpha_{1,1}$, $S(q_1, k_2)$ yields $\alpha_{1,2}$, and so on.
- $\alpha_{1,i}$ = $ q_1 \cdot k_i / \sqrt{d}$
- $d$ represents the dimensions of $q$ and $k$. This is a trick used by the authors in the paper.
- Followed by Softmax normalization to normalize the values.
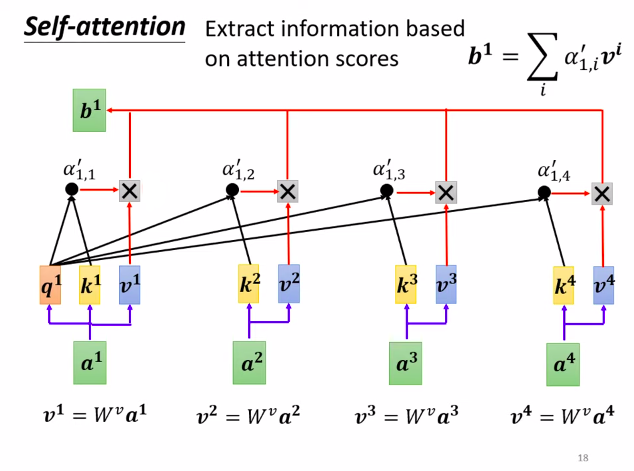
- Multiply the obtained $\hat{\alpha}$ with $v$ to get $b$, which is equivalent to a weighted sum.
- The obtained $b_1$ in the figure is the first vector (word or character) of the sought sequence.
- Each output vector incorporates information from the entire sequence.
Prallel Processing
$$q_i = W^qa_i$$
$$k_i = W^ka_i$$
$$v_i = W^va_i$$
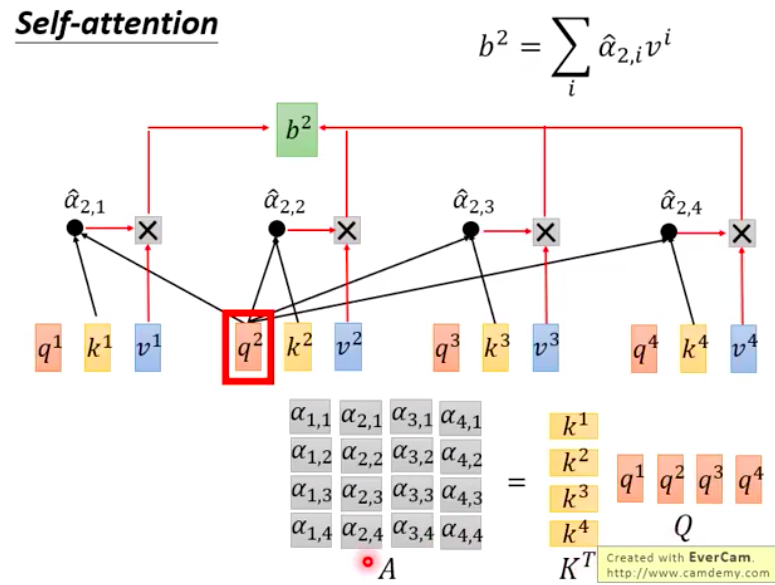
- Consider $a_1$, …, $a_4$ as a matrix $I$. Multiply it by the weight matrix $W^q$ to obtain $q_1$, …, $q_4$, forming another matrix $Q$.
- The same process applies to matrices $K$ and $V$, formed by multiplying $q$, $k$, and $a$ to get
$\alpha_{1,1}$ = $k^T_1 \cdot q_1$,
$\alpha_{1,2}$ = $k^T_2 \cdot q_1$,
…
Stack $k_1$, …, $k_4$ to form matrix $K$, then multiply it by $q_1$ stacked with $q_2$, …, $q_4$ to form matrix $Q$, resulting in a matrix $A$ composed of $\alpha$ values, which is the Attention. - After applying Softmax, it becomes $\hat{A}$. In each time step, attention exists between each pair of vectors.
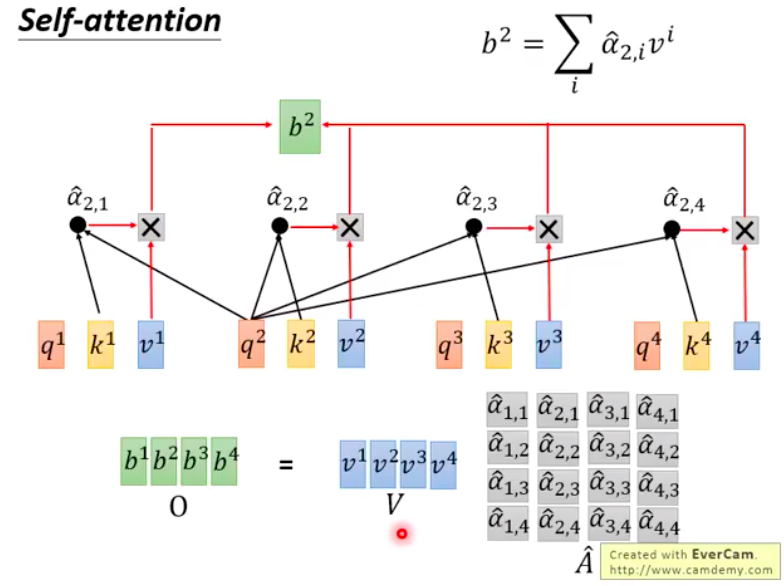
By calculating the weighted sum of $V$ and $\hat{A}$, you obtain $b$, and the matrix composed of b forms the output matrix $O$.”
What self-attention layer do
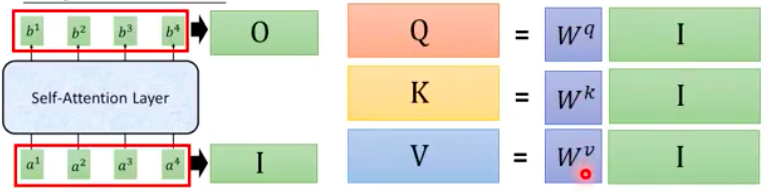
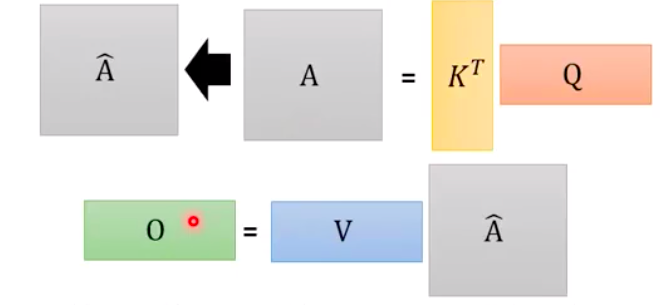
By converting it into matrix multiplication, you can utilize the GPU to accelerate the computation.
Multi-head Self-attention
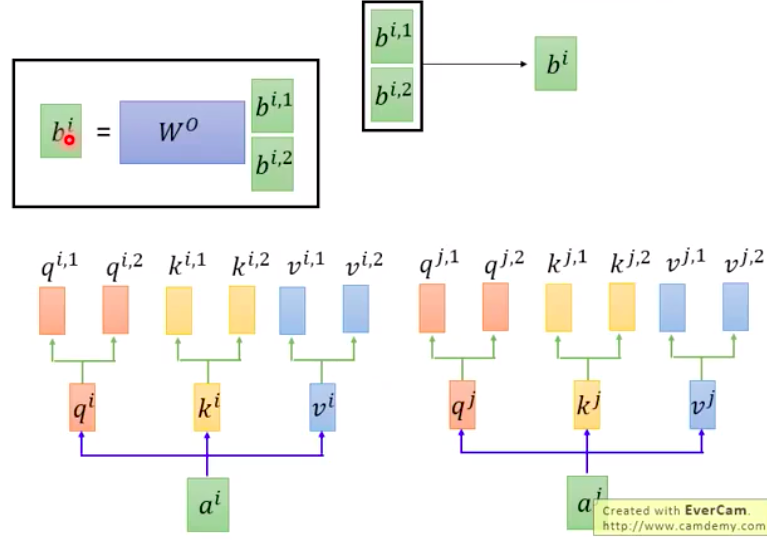
Taking 2 heads as an example:
- Having 2 heads means splitting $q, k, v$ into two sets of $q, k, v$. And $q_{i,1}$ will only be multiplied with $k_{i,1}$ to obtain $\alpha_{i,1}$, finally calculating $b_{i,1}$.
- Afterward, concatenate $b_{i,1}, b_{i,2}$, apply a transformation, and perform dimension reduction to obtain the final $b_i$.
- Each head focuses on different information; some only care about local information (neighborhood data), while others concentrate on global (long-term) information, and so on.
Positional Encoding
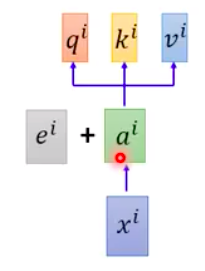
In the attention mechanism, the order of words in the input sentence doesn’t matter.
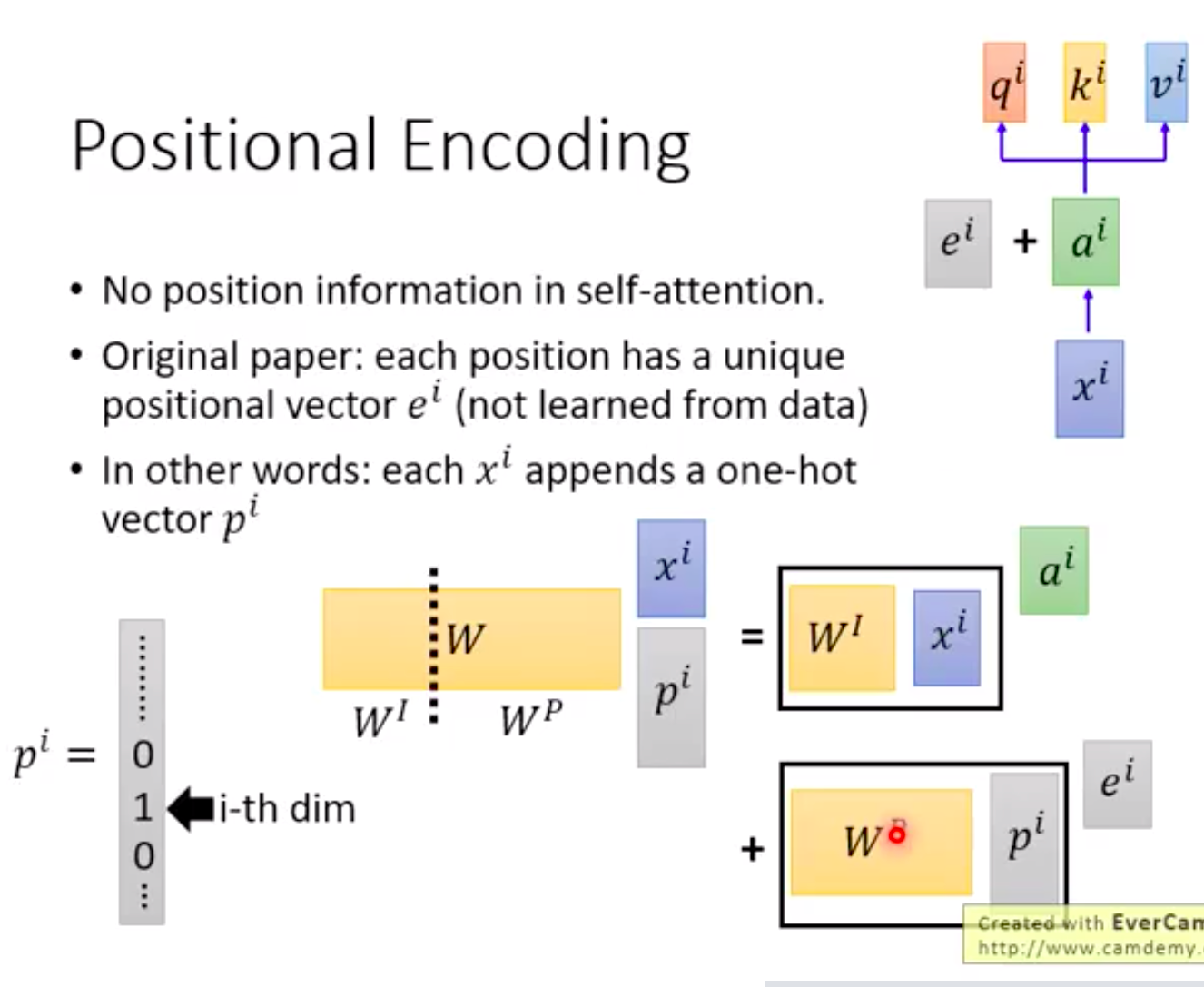
- Without positional information => Therefore, there is a unique position vector $e_i$, which is not learned but set by humans.
- Other methods: Using one-hot encoding to represent $p_i$ as $x_i$ to denote its position.
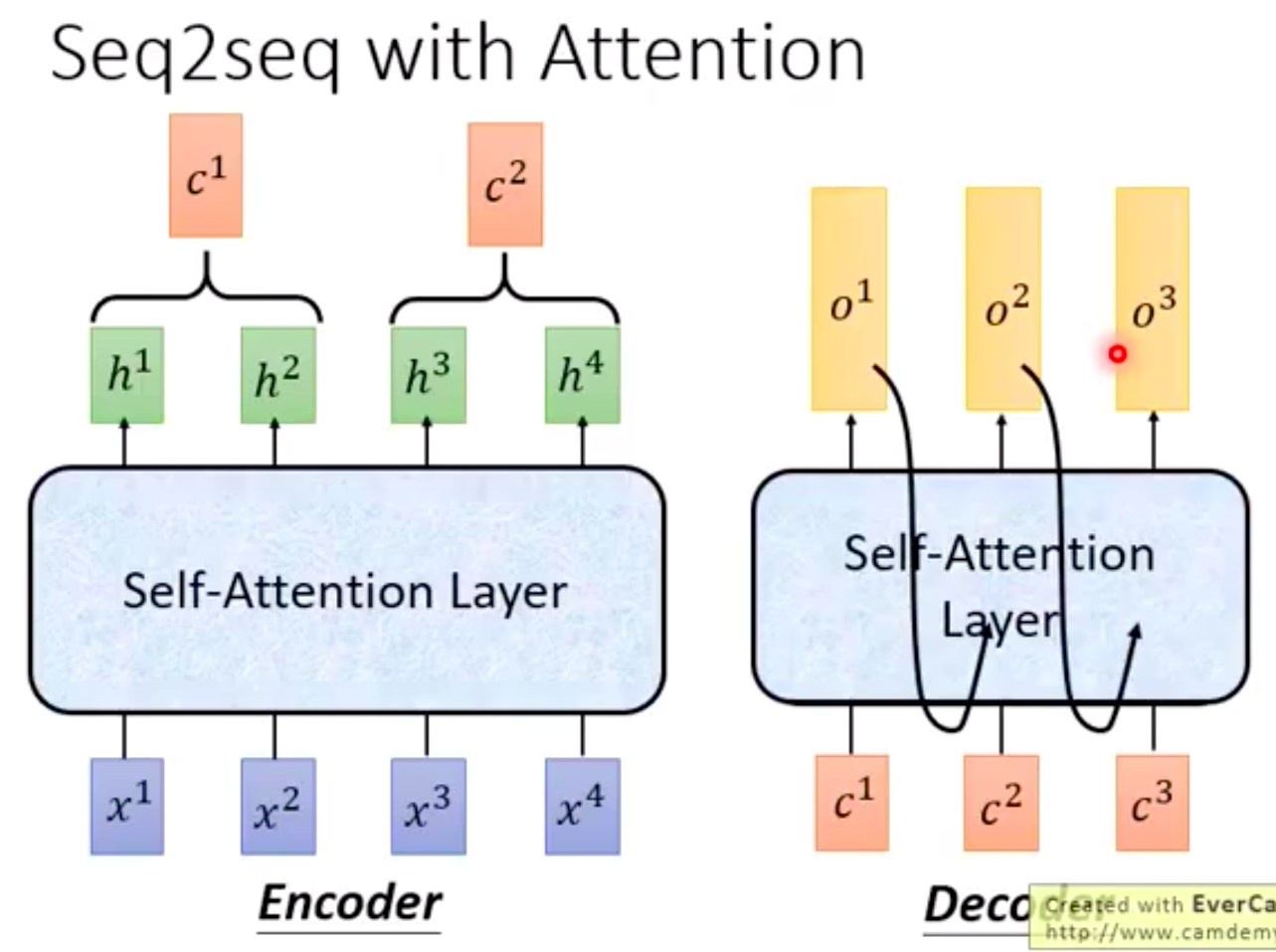
Seq2seq with Attention
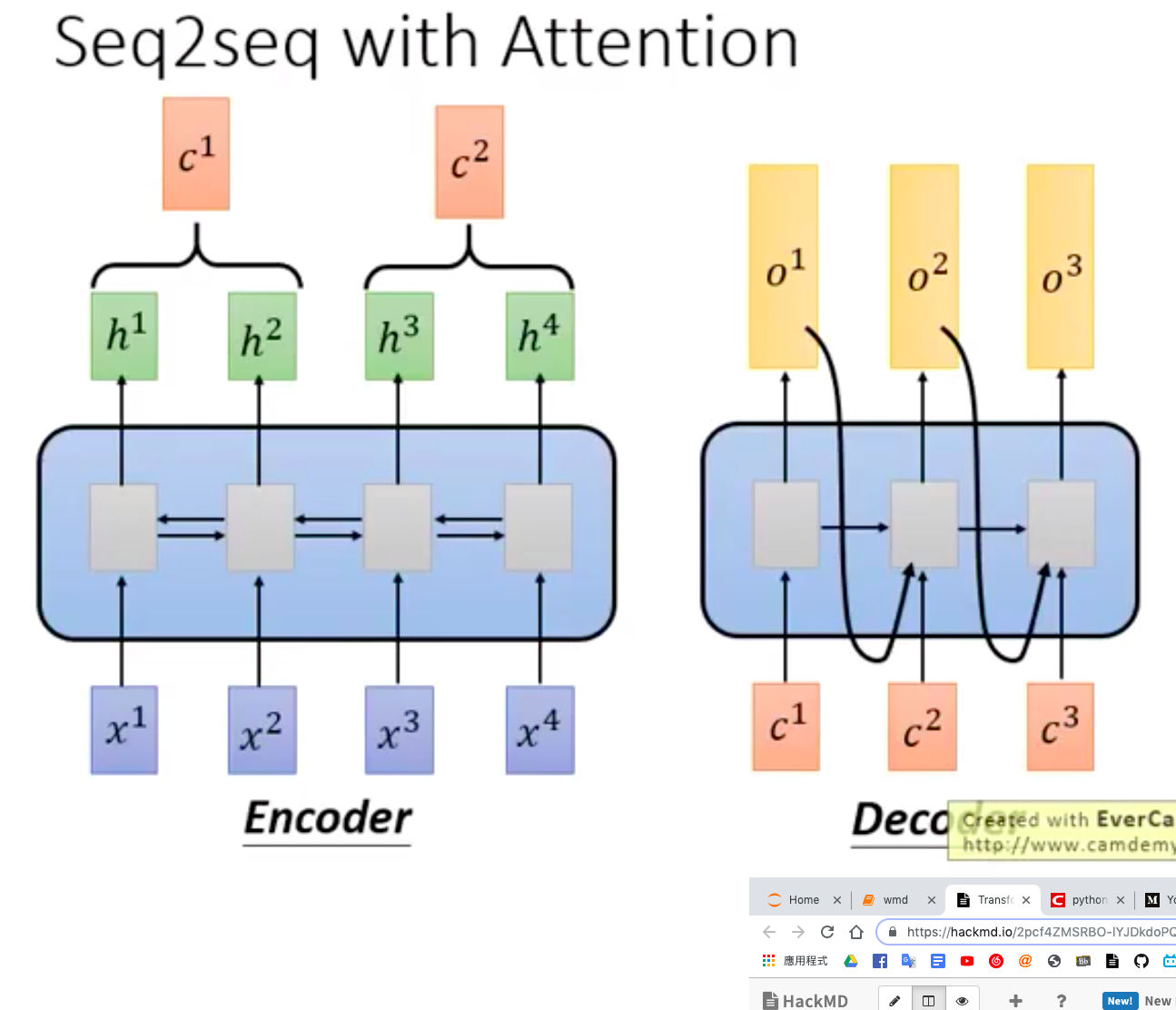
The original seq2seq model consists of two RNNs, an Encoder and a Decoder, and can be applied to machine translation.
In the diagram above, the Encoder originally contained bidirectional RNNs, while the Decoder contained a unidirectional RNN. In the diagram below, both(bi/unidirectional RNN) have been replaced with Self-Attention layers, achieving the same purpose and enabling parallel processing.
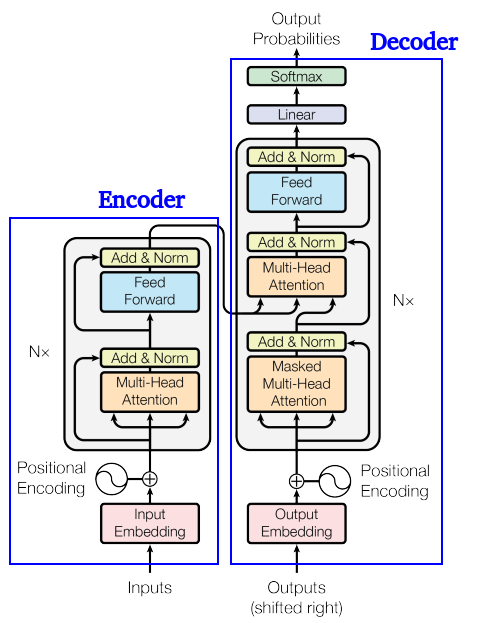
Look into the detail of Transformer Model

Using Chinese to English translation for example.
Encoder Part:
- The input goes through Input Embedding, which considers positional information and is augmented with manually set Positional Encoding. It then enters the block that repeats N times.
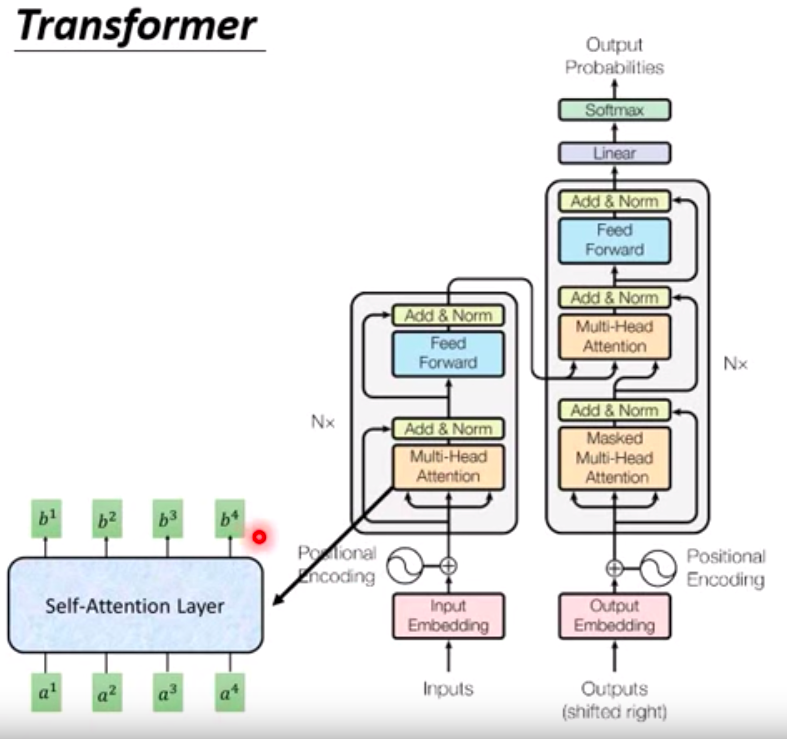
- Multi-head:
Within the Encoder, it utilizes Multi-head Attention, which means there are multiple sets of $q$, $k$, $z$. Inside this mechanism, individual $qkv$ multiplications with $a$ are performed, leading to the calculation of $\alpha$, ultimately resulting in $b$.
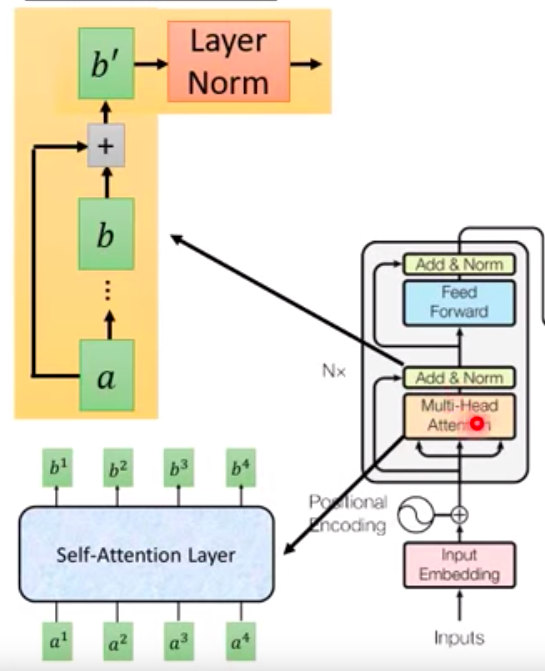
- Add & Norm (residual connection):
The input of Multi-head Attention, denoted as $a$, is added to the output $b$, resulting in $b^\prime$. Following this, Layer Normalization is performed. - Once the calculations are completed, the result is passed through the forward propagation, followed by another Add & Norm step.
Decoder Part
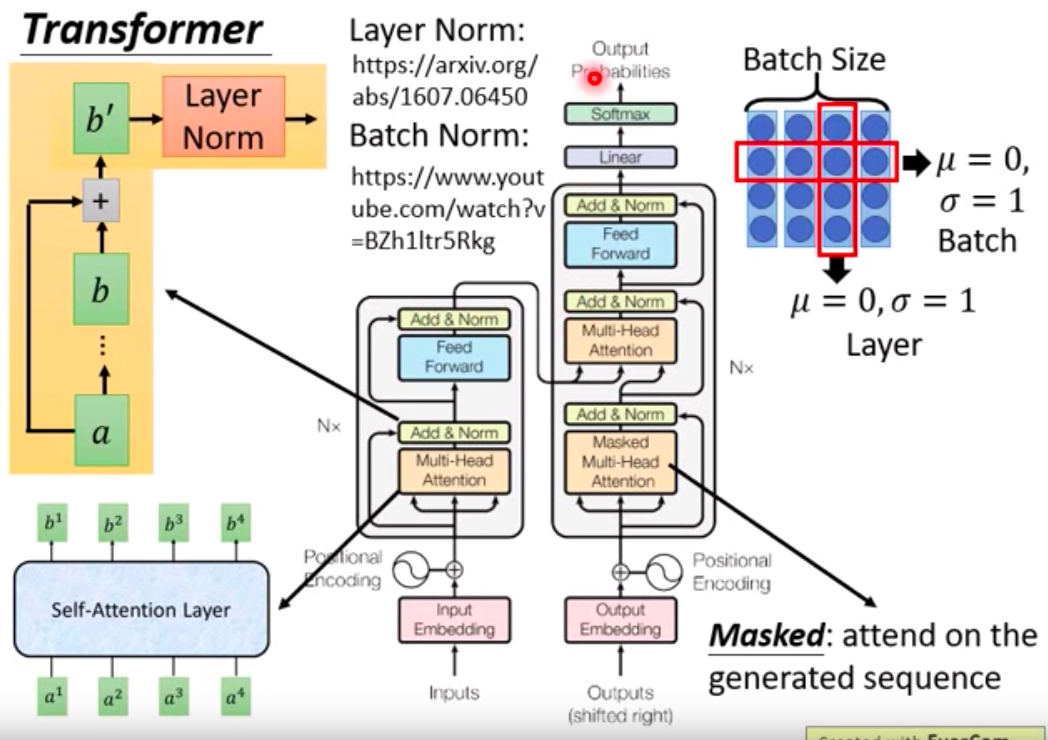
The Decoder input is the output from the previous time step. It goes through output embedding, considering positional information, and is augmented with manually set positional encoding. It then enters the block that repeats n times.
Masked Multi-head Attention:
Attention is performed, where “Masked” indicates attending only to the already generated sequence. This is followed by an Add & Norm layer.Next, it undergoes a Multi-head Attention layer, attending to the previous output of the Encoder, followed by another Add & Norm layer.
After the computations, it is passed to the Feed Forward forward propagation. Subsequently, Linear and Softmax operations are applied to generate the final output.
Last but not least, I provide the definition and purpose of encoder and decoder (in the previous article):
Encoder-Decoder Architecture:
The Transformer’s architecture is divided into an encoder and a decoder. The encoder processes the input sequence, capturing its contextual information, while the decoder generates the output sequence. This architecture is widely used in tasks like machine translation.
Attention Visualization
single-head
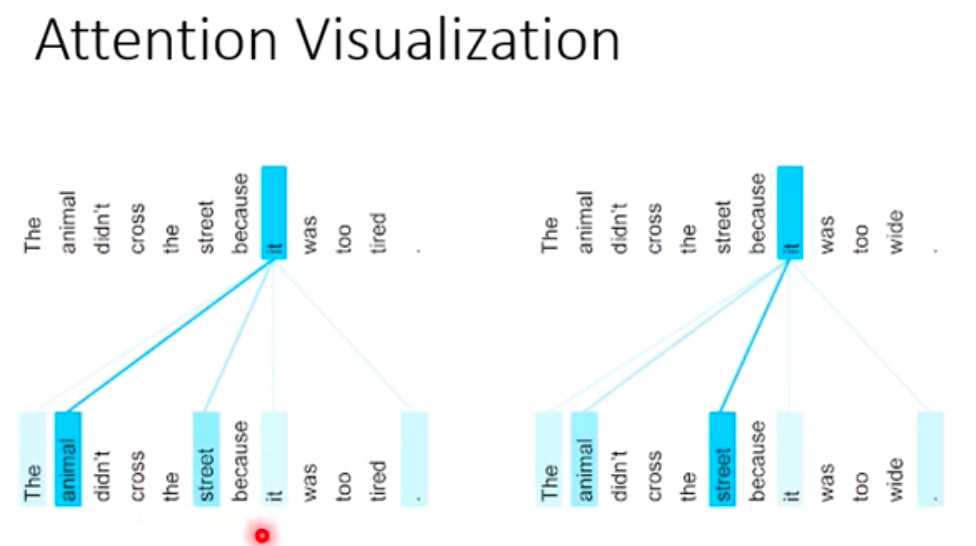
The relationships between words. The thicker the line, the more related of these words.
multi-head
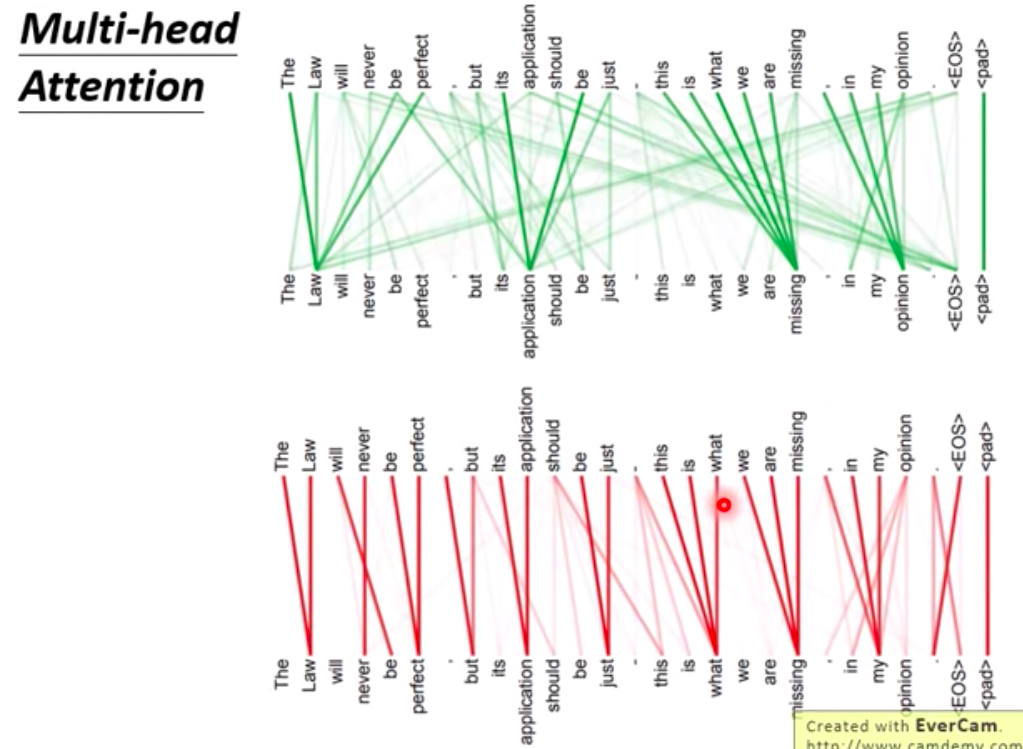
The results obtained by pairing different sets of $q$ and $k$ vectors differ, indicating that different sets of $q$ and $k$ possess distinct information. This signifies that various sets of $q$ and $k$ hold different types of information, with some focusing on local aspects (below) and others on global aspects (above).
Reference
- 3Blue1Brown
- iThome - Day 27 Transformer (Recommend)
- iThome - Day 28 Self-Attention (Recommend)
- Transformer 李宏毅深度學習 (Recommend)
- Transformer 李宏毅老師簡報
- 李宏毅老師YouTube channel
- Attention is all you need (paper)
