[NLP][ML] Transformer (2) - Attention & Summary
Overview
Self-attention allows the model to weigh the importance of different parts of an input sequence against each other, capturing relationships and dependencies between elements within the sequence. This is particularly powerful for tasks involving sequential or contextual information, such as language translation, text generation, and more.
What Self-Attention wants to do is to replace what RNN can do
Its output/input is the same as RNN, and its biggest advantages are:
- Can parallelize operations
- Each output vector has seen the entire input sequence. So there is no need to stack several layers like CNN.
Difference between attention and self-attention
attention is a broader concept of selectively focusing on information, while self-attention is a specific implementation of this concept where elements within the same sequence are attended to. Self-attention is a fundamental building block of the Transformer architecture, allowing it to capture relationships and dependencies within sequences effectively.
Attention (Machanism)
main idea:
use triples
$$<Q,K,V>$$
Represents the attention mechanism, expresses the similarity between Query and Key, and then assigns the value of Value according to the similarity
formula:
$$Attention(Q,K,V) = softmax(\frac{QK^T}{\sqrt{d_k}})V$$
Self-Attention(Layer) (Key)
Computing process
Now we suppose to enter $a_1$~$a_4$ Four vector, and Self-Attention needs to output another row of $b$ vectors, and each $b$ is generated after considering all $a$
To figure out $b_1$, the first step is based on $a_1$, find other vectors related to $a_1$ in this sequence. We use the “$\alpha$” to represent the similarity of each vector related to $a_1$.
It must be mentioned here that there are 3 very important values in the Self-Attention mechanism: Query, Key, Value. Respectively represent the value used to match, the value to be matched, and the extracted information.
As for determining the correlation between two vectors, the most commonly used method is the dot product (here is scaled dot product). It takes two vectors as input and multiplies them with two different matrices. The left vector is multiplied by the matrix $W^q$ (Query matrix), and the right vector is multiplied by the matrix $W^k$ (Key matrix). The values of $W^q$ and $W^k$ are both randomly initialized and obtained through training.
Next, after obtaining the two vectors, $q$, $k$, the dot product is computed between them. After summing up all the dot products, a scalar (magnitude) is obtained. This scalar is represented as $\alpha$, which we consider as the degree of correlation between the two vectors.
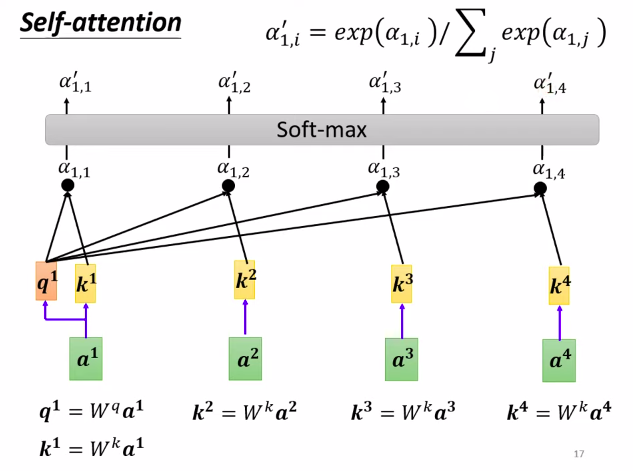
Next, we apply what was just introduced to Self-Attention.
- First, we calculate the relationships “$\alpha$” between $a_1$ and $a_2$, $a_3$, $a_4$ individually.
- We multiply $a_1$ by $W^q$ to obtain $q_1$.
- Then, we multiply $a_2$, $a_3$, $a_4$ by $W^k$ respectively and compute the inner products to determine the relationship “$\alpha$” between $a_1$ and each vector.
- Applying the Softmax function yields $\alpha’$.
- With this $\alpha’$, we can extract crucial information from this sequence!
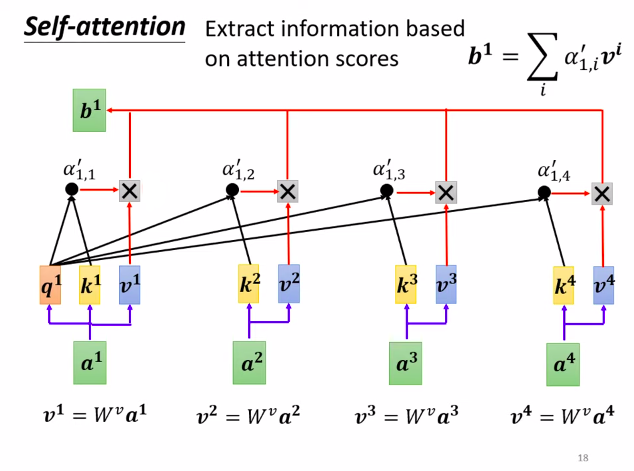
- How to extract important information using $\alpha’$? The steps are as follows:
- First, multiply $a_1$ ~ $a_4$ by $W^v$ to obtain new vectors, denoted as $v_1$, $v_2$, $v_3$ and $v_4$, respectively (where $W^v$ is the Value matrix).
- Next, multiply each vector here, $v_1$ ~ $v_4$, by $\alpha’$, and then sum them to obtain the output $b_1$ (formula written in the top-right corner of the image).
If a certain vector receives a higher score - for instance, if the relationship between $a_1$ and $a_2$ is strong, leading to a large value for $\alpha_{1,2}’$ - then after performing the weighted sum, the value of $b_1$ obtained could be very close to $v_2$.
Now that we know how to compute $b_1$, it naturally follows that we can deduce $b_1$, $b_2$, $b_3$, and $b_4$ using the same method. With this, we have completed the explanation of the internal computation process of Self-Attention.
Last but not least, the similarity matrix($\alpha_{i,j}$) is just the attention in the self-attention layer, i.e. importance or relevance to other elements in the same sequence..
Summary
Attention (Score, Weight and Output)
- $ Attention Score = QK^T $
- $ Attention Weights = Softmax(\frac{Attention Score}{\sqrt{d_k}}) $
- $ Attention Output = (Attention Weights)V $
Key Components of Transformers
Self-Attention Mechanism:
The core innovation of the Transformer is the self-attention mechanism, which allows the model to weigh the importance of different words in a sequence relative to each other. It computes attention scores for each word by considering its relationships with all other words in the same sequence. Self-attention enables capturing context and dependencies between words regardless of their distance.Multi-Head Attention:
To capture different types of relationships, the Transformer employs multi-head attention. Multiple sets of self-attention mechanisms (attention heads) run in parallel, and their outputs are concatenated and linearly transformed to create a more comprehensive representation.Positional Encodings:
Since the Transformer does not inherently understand the order of words in a sequence (unlike recurrent networks(RNN)), positional encodings are added to the input embeddings. These encodings provide information about the positions of words within the sequence.Encoder-Decoder Architecture:
The Transformer’s architecture is divided into an encoder and a decoder. The encoder processes the input sequence, capturing its contextual information, while the decoder generates the output sequence. This architecture is widely used in tasks like machine translation.Residual Connections and Layer Normalization:
To address the vanishing gradient problem, residual connections (skip connections) are used around each sub-layer in the encoder and decoder. Layer normalization is also applied to stabilize the training process.Position-wise Feed-Forward Networks:
After the self-attention layers, each position’s representation is passed through a position-wise feed-forward neural network, which adds non-linearity to the model.Scaled Dot-Product Attention:
The self-attention mechanism involves computing the dot product of query, key, and value vectors. To control the scale of the dot products and avoid large gradients, the dot products are divided by the square root of the dimension of the key vectors.Masked Self-Attention in Decoding:
During decoding, the self-attention mechanism is modified to ensure that each position can only attend to previous positions. This masking prevents the model from “cheating” by looking ahead in the output sequence.Transformer Variants:
The original Transformer model has inspired various extensions and improvements, such as BERT, GPT, and more. BERT focuses on pretraining language representations, while GPT is designed for autoregressive text generation.
The Transformer architecture has become the foundation for many state-of-the-art NLP models due to its ability to capture context, parallelize computations, and handle long-range dependencies effectively. It has led to significant advancements in machine translation, text generation, sentiment analysis, and various other NLP tasks.
Reference
- 3Blue1Brown
- iThome - Day 27 Transformer (Recommend)
- iThome - Day 28 Self-Attention (Recommend)
- Transformer 李宏毅深度學習 (Recommend)
- Transformer 李宏毅老師簡報
- 李宏毅老師YouTube channel
- Attention is all you need (paper)
